彩蛋
先无理解的背诵一下吧,感觉离散学起来确实是枯燥

1.1命题符号化及联结词
命题与真值
简单命题
复合命题
联结词
命题:判断结果惟一的陈述句
命题的真值:判断的结果
真值的取值:真、假
真命题:真值为真的命题
假命题:真值为假的命题
注:
1、感叹句、祈使句、疑问句都不是命题
2、陈述句中的悖论以及判断结果不唯一的也不是命题
命题的分类:
简单命题(原子命题):简单陈述句构成的命题
复合命题:由简单命题与联结词按一定规则复合而成的命题
联结词与复合命题

例:将下列命题符号化
(1)王晓既用功又聪明
(2)王晓不仅聪明,而且用功
(3)王晓虽然聪明,但不用功
(4)张辉与王丽都是三好生
(5)张辉与王丽是同学


注:
描述合取式的灵活性与多样性
分清简单命题与复合命题

例:将下列命题符号化
(1)2或4是素数
(2)2或3是素数
(3)4或6是素数
(4)小元只能拿一个苹果或一个梨
(5)王晓红生于1975年或1076年


“如果p,则q”的不同表述很多:
若p,就q
只要p,就q
p仅当q
只有q才p
除非q,才p
除非q,否则非p(双重否定)

例题:经典


1.2命题公式及分类
命题变项与合式公式
公式的赋值
真值表
公式的类型:重言式、矛盾式、可满足式
真值函数
命题变项与合式公式
命题常项:简单命题
命题变项:真值不确定的陈述句
定义 合式公式(命题公式,公式)递归定义如下:

公式的赋值
定义 给公式A中的命题变项 p1, p2, … , pn指定
一组真值称为对A的一个赋值或解释
成真赋值: 使公式A为真的赋值
成假赋值: 使公式A为假的赋值
公式的类型
定义:设A为一个命题公式
(1)若A无成假赋值,则称A为重言式(也称永真式)
(2)若A无成真赋值,则称A为矛盾式(也称永假式)
(3)若A不是矛盾式,则称A为可满
析取范式与合取范式
简单析取式:有限个命题变项或其否定构成的析取式
简单合取式:有限个命题变项或其否定构成的合取式
析取范式:由有限个简单合取式组成的析取式
合取范式:由有限个简单析取式组成的合取式

范式只有三个符号,合取,析取,和否定,简要来说就是“与或非”
找范式的步骤:
①去掉–>和<–>符号
②德摩根律
③结合律&分配律
化简成析取范式&合取范式

析取范式与合取范式不唯一
极小项与极大项 m&M
主析取范式与主合取范式
m1的否定就是M1,mi的否定就是Mi
由极小项构成的析取范式就是主析取范式
由极大项构成的合取范式就是主合取范式

主析取范式和主合取范式都是唯一的
第二步是关键 无中生有的操作
二进制的基本计算方式


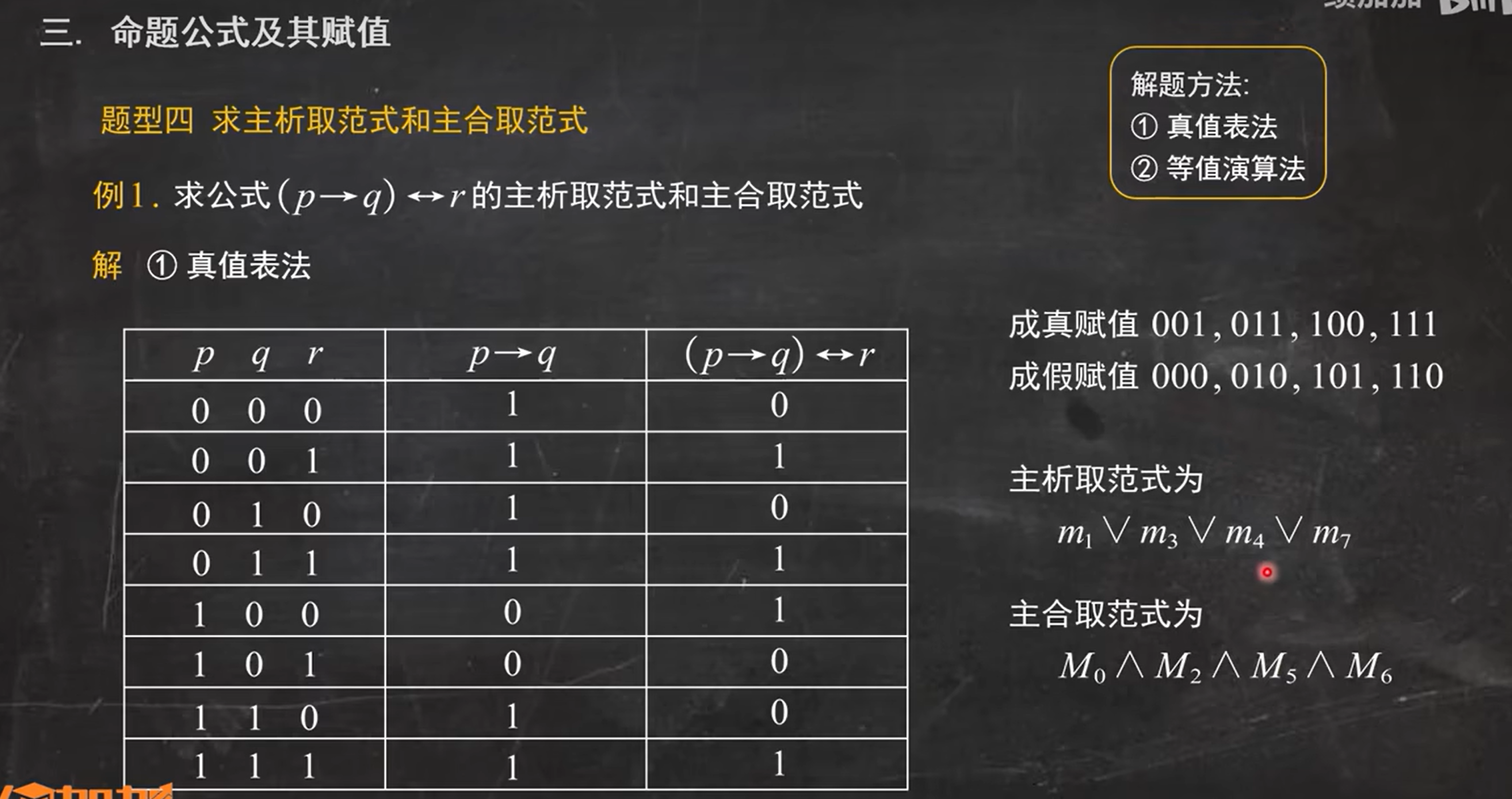
找主析取范式&主合取范式的方法:①公式的等值演算 ②真值表
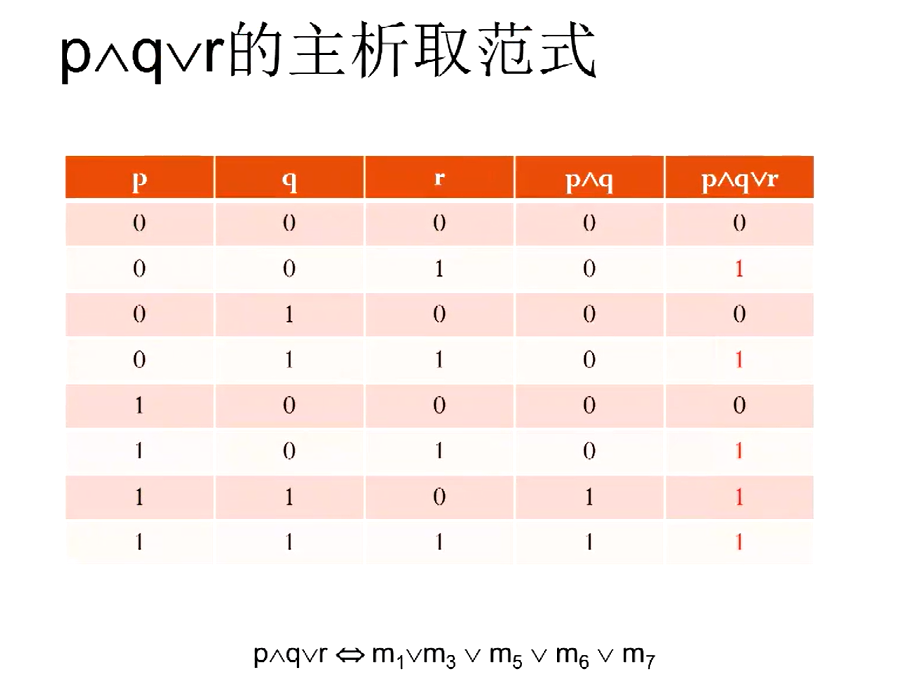
找他的成真赋值即可
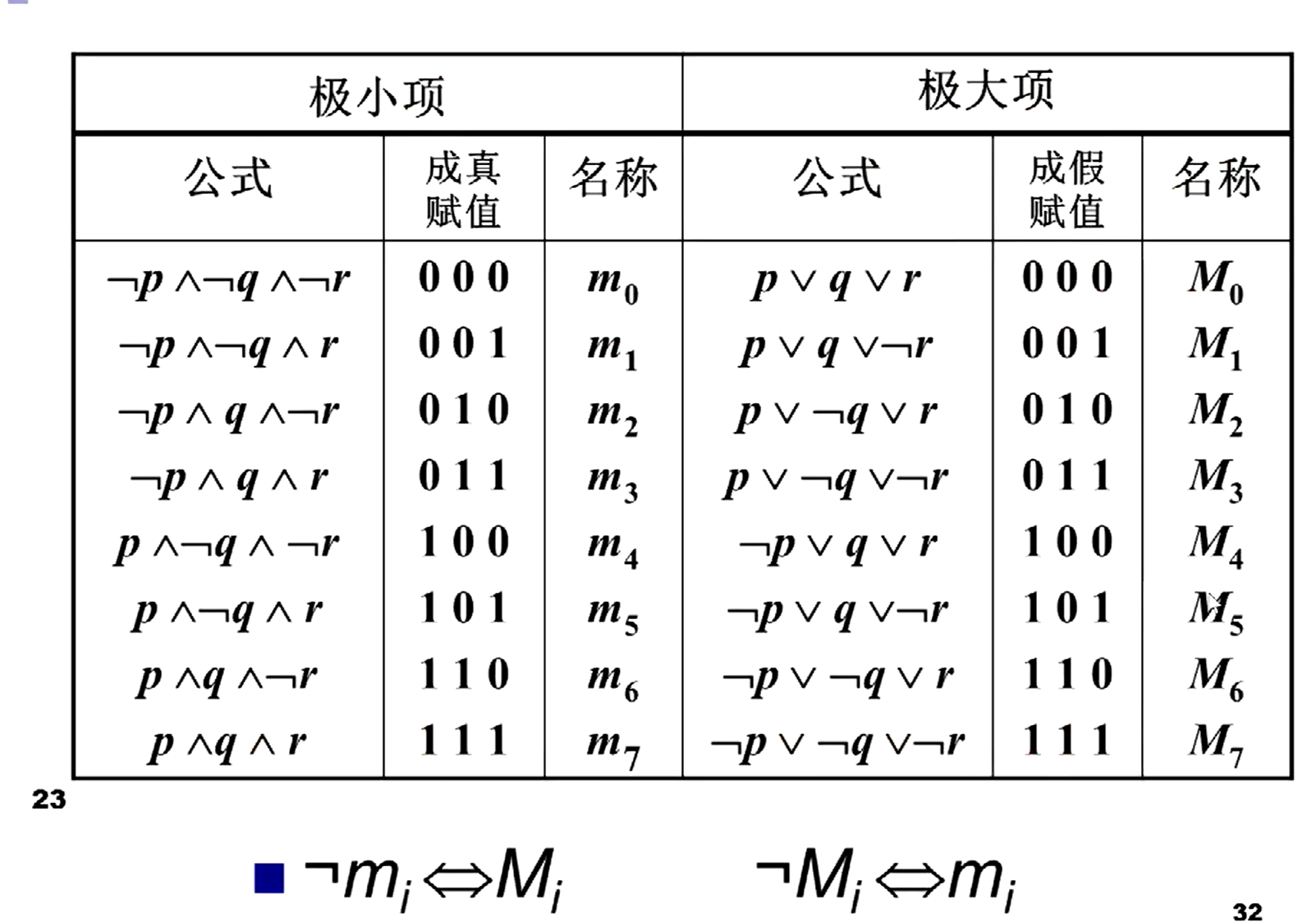
主合取范式求极小项,主析取范式求极大项

逻辑联结词的全功能集
只有交,并两个联结词是不行的
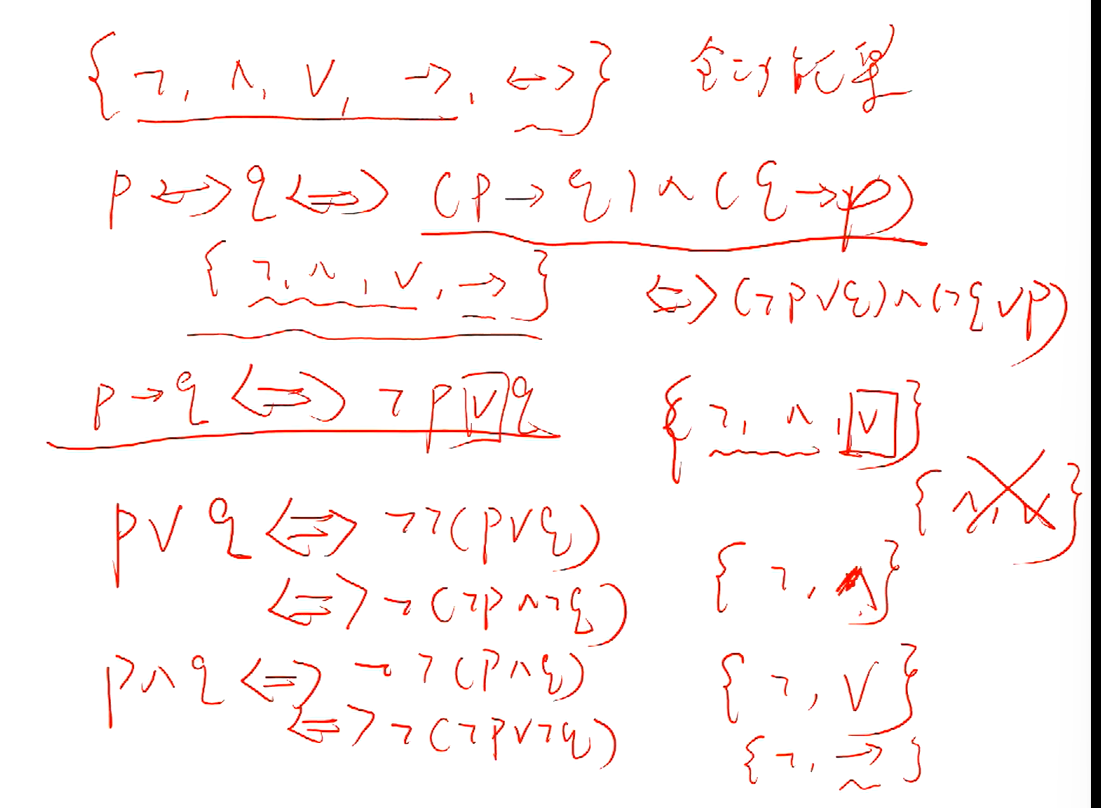
复合联结词
 –+
–+
与非 p↑q
或非 p↓q
德摩根律和否定之否定
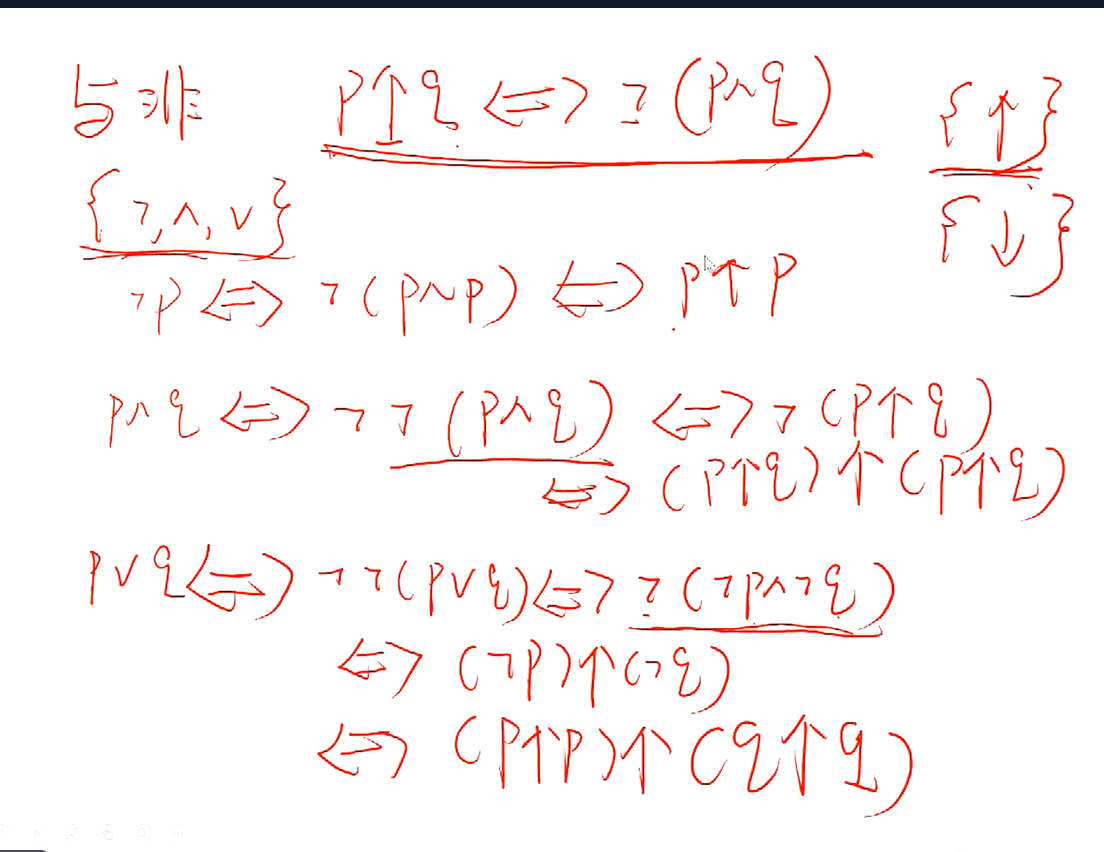
推理理论
从已知得到结论
判断推理是否正确的方法


这题的解题点,相当于要去证明绿色框框里面的式子是永真式,第一个最直接的方法我们可以使用真值表法来解决 ,第二个方法我们也可以用等值演算去进行推理,最终得出这个式子是永真式。
推理定律——重言蕴含式
重要,要记


这些推理成立的本质是什么,比如说这里的假言推理,可以经过之前学过的等值演算进行化简,最后得到的式子其实就是B,A直接都被化简掉了
直接证明法


附加前提证明法


归谬法(反证法)

一阶逻辑


表示性质的一般是一元谓词,表示相互关系的一般是多元谓词

谓词逻辑的符号化
“ 仅当”是蕴含的意思 –>





辖域&自由出现& 变元の判断

例题:
管辖范围内出现的变量肯定是约束的,看辖域主要就是看括号就可以了

一阶逻辑等值式与前束范式
逻辑有效式–>永真

集合论
空集是任何集合的子集

A的所有子集构成的集合
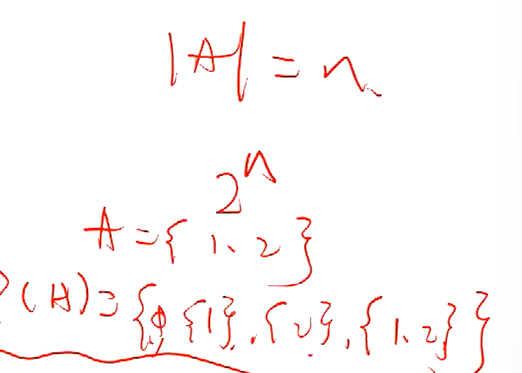
空集的幂集就一个元素,也就是空集本身

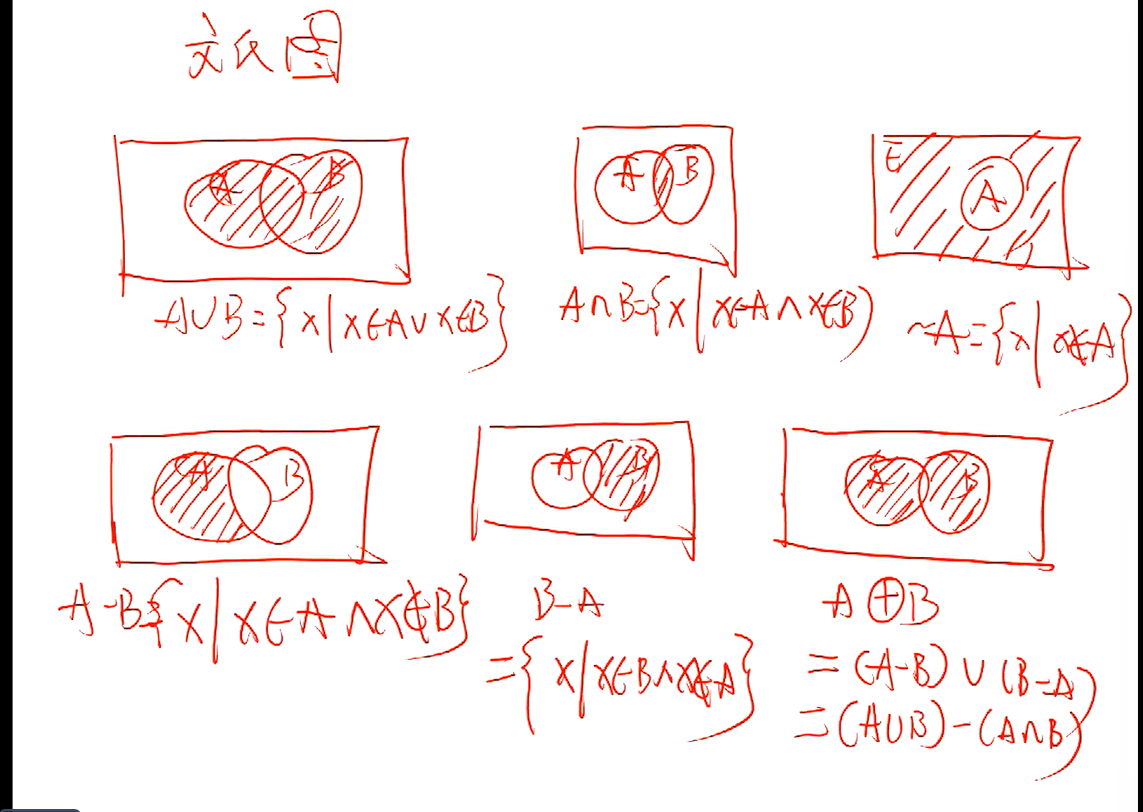
文氏图
二元关系与函数



笛卡尔积首先是一个集合

空集与任何一个集合作笛卡尔积的结果是空集
传递闭包的计算

离散数学中与线性代数矩阵相关的计算,这里的R中包含的值,比如说第一行的0100,分别是aa,ab,ac,ad,而在R中只有ab,所以只有第二列是1,是这么个逻辑
方法:作矩阵的乘法运算
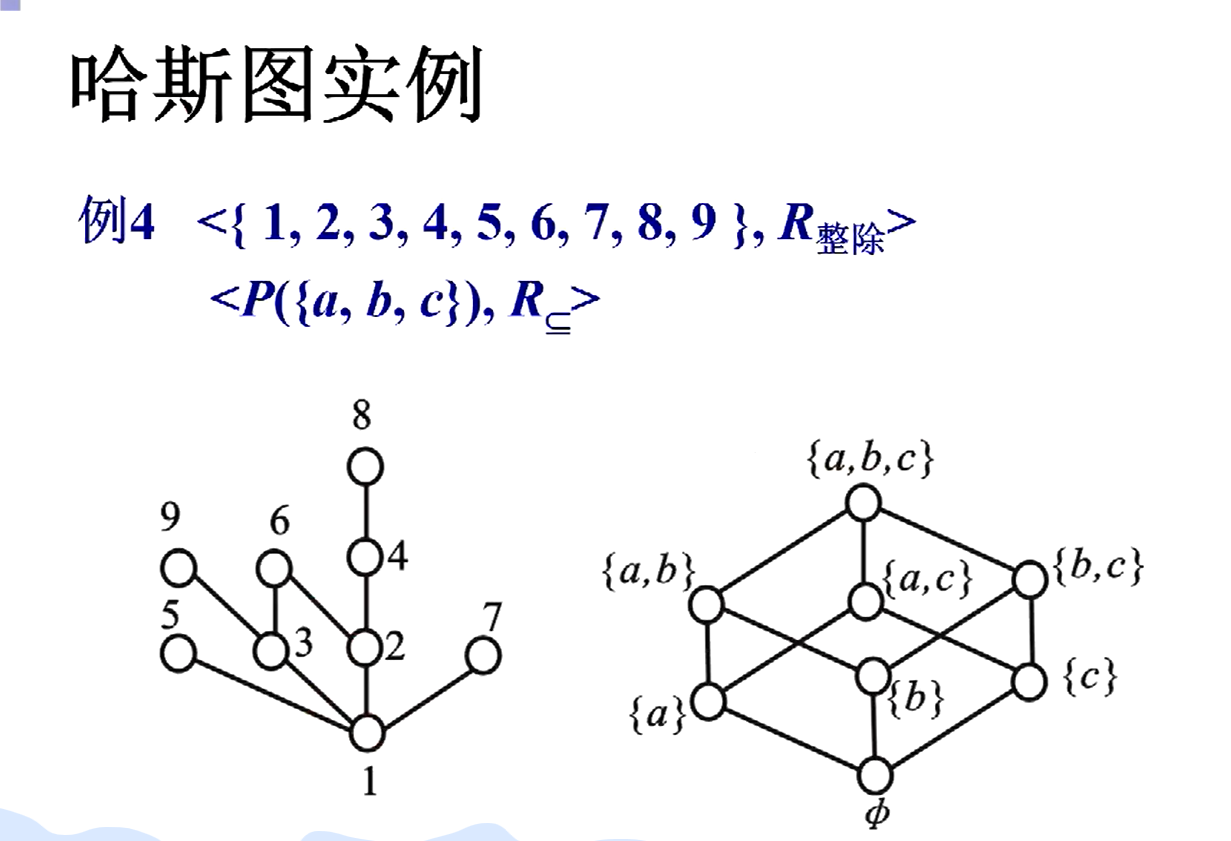
哈斯图的绘制
哈斯图针对自反,反对称,传递等性质,自反的圈圈可以省略,反对称肯定是单线,传递的第三条线可以直接省略。
自反意味着每个点都有自回路
反对称意味着两点之间有线的话一定是单线
构成一个三角形的回路,ab,bc,ac构成传递
ab有,bc有,ac就可以省略

实例:6和4没有关系,什么叫做覆盖,就是数字在上面
例题*2:


根据哈斯图写出表达式
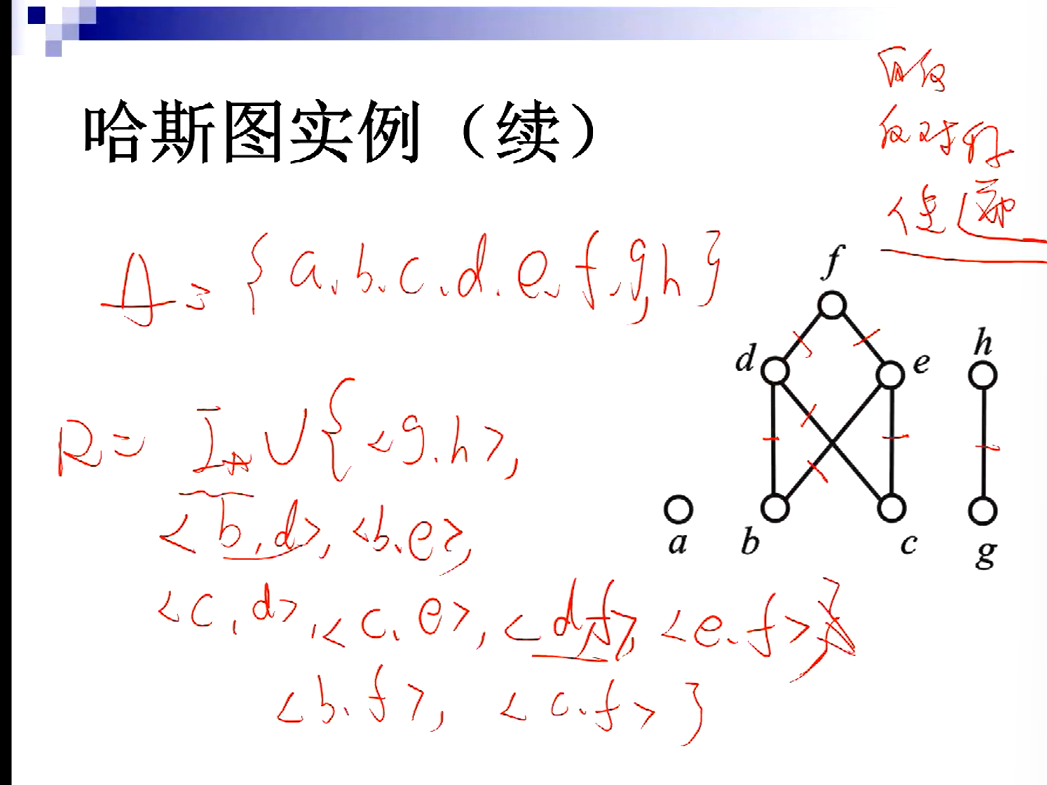
IA是自回路,传递性生出的第三条边也要记得写上
极小元,极大元,上界,下界,上确界,下确界
极小元不一定小于极大元

对于有穷集,极小元和极大元必存在,可能存在多个。
最小元和最大元不一定存在,如果存在一定唯一
最小元一定是极小元;最大元一定是极大元
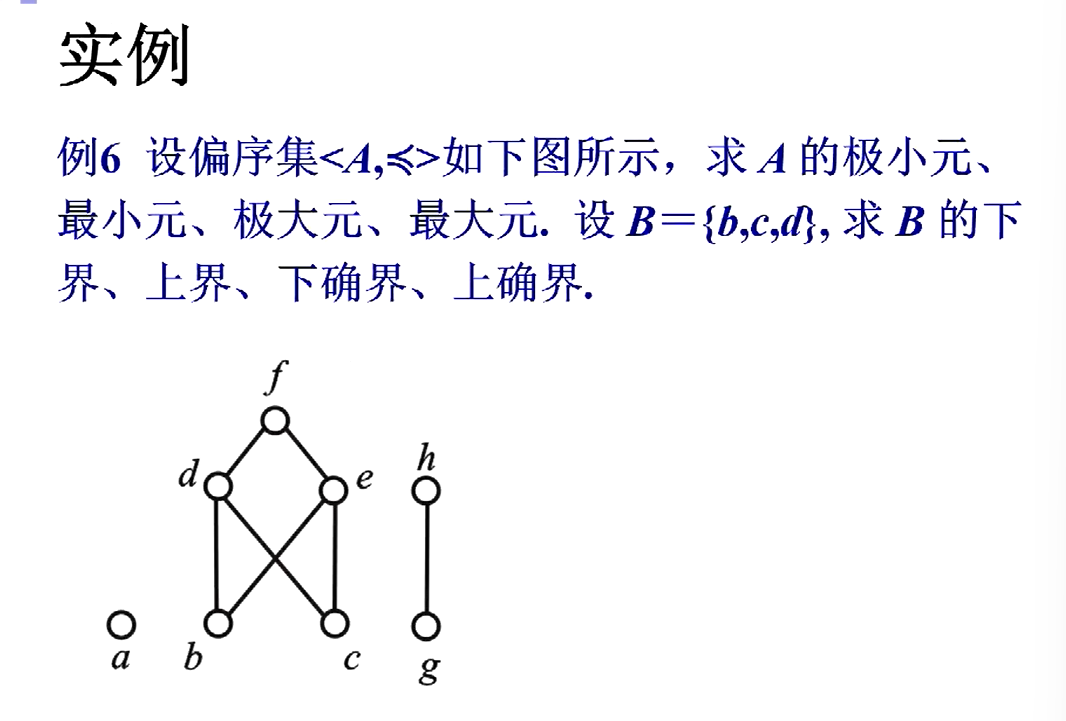
(1)
极小元:g,a,b,c
极大元:a,h,f
最大元:不存在
最小元:不存在
(2)
下界:无
上界:f,d
下确界:无
上确界:d
通路与回路
G=<V,E>,图的表现形式,V是点的集合,E是边的集合
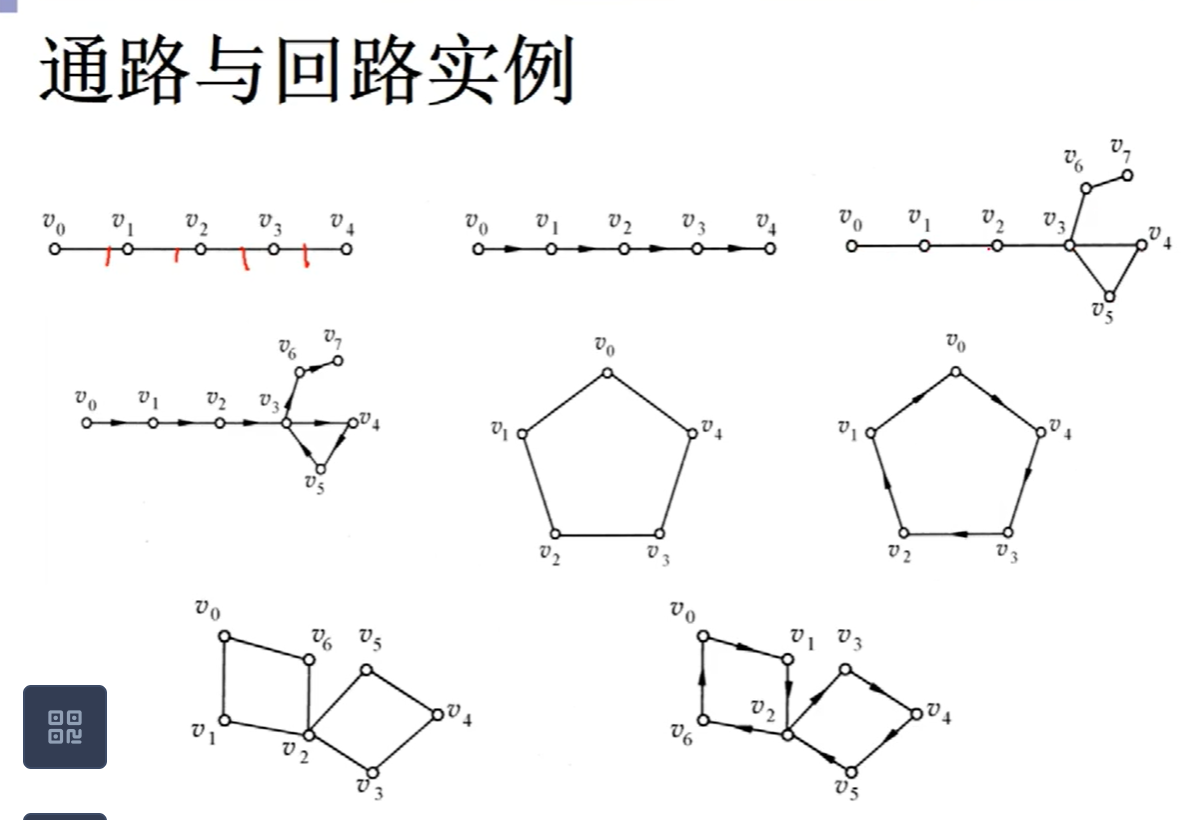
通路与回路的表示方法

简单图里面直接用点表示就可以了,简单图是没有重边和圈的图,圈的长度是1
在无向简单图中,所有圈的长度≥3,;在有向简单图中,所有圈的长度≥2


0图,只有点的图,空图,什么都没有的图,平凡图,只有一个点的图
连通关系是一种等价关系
等价关系可以做划分,所以连通关系也可以做划分
点割集
删掉一个点,不仅要删掉这个点,还要删掉与这个点相邻的两条边
删掉一条边,只删掉边,点是要保留的
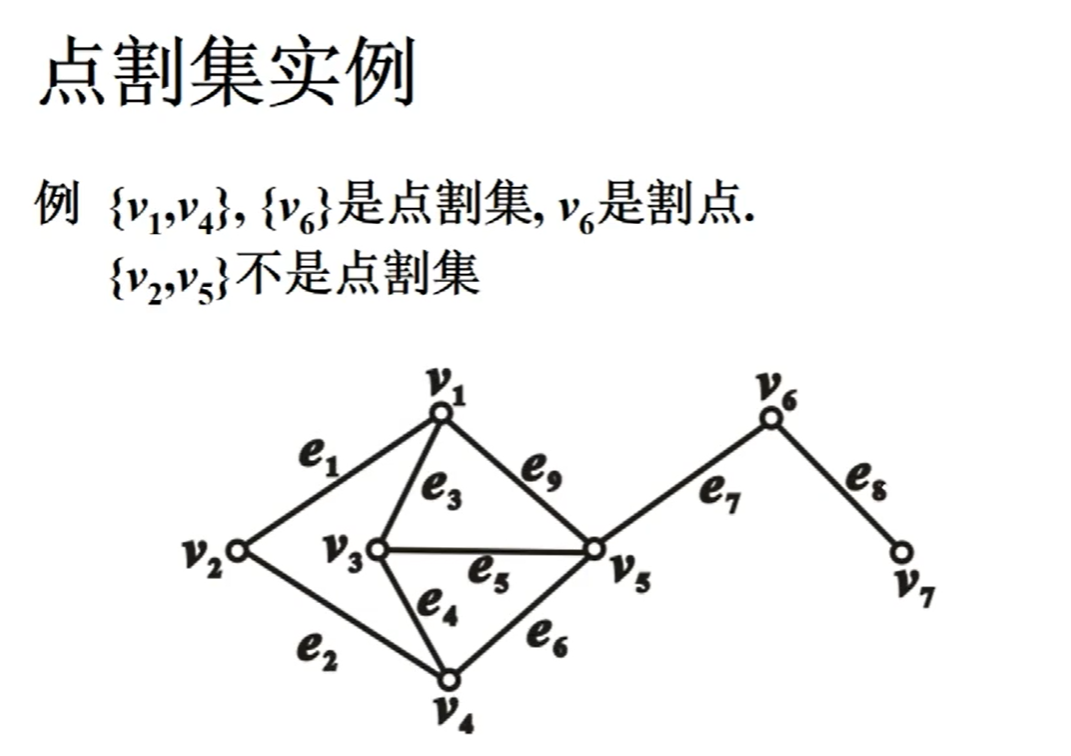
点割集:可以将这个图断开来的点的集合
边割集

比如说上张图里的割边,就有e7,e8,边割集有比如说{e1,e2}
Kn是什么?是n阶完全图,任何一个节点,都和另外的节点相连
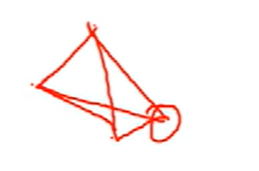
这是K4图
有向图的连通性
自反,传递,但没有对称性,不是等价关系
基图:有向图去掉方向得到的无向图叫做基图
图的矩阵表示
无向图的关联矩阵
有向图的关联矩阵
有向图的邻接矩阵
有向图的可达矩阵

有三种表示方式,代数表示,图的表示,矩阵表示
无向图的关联矩阵
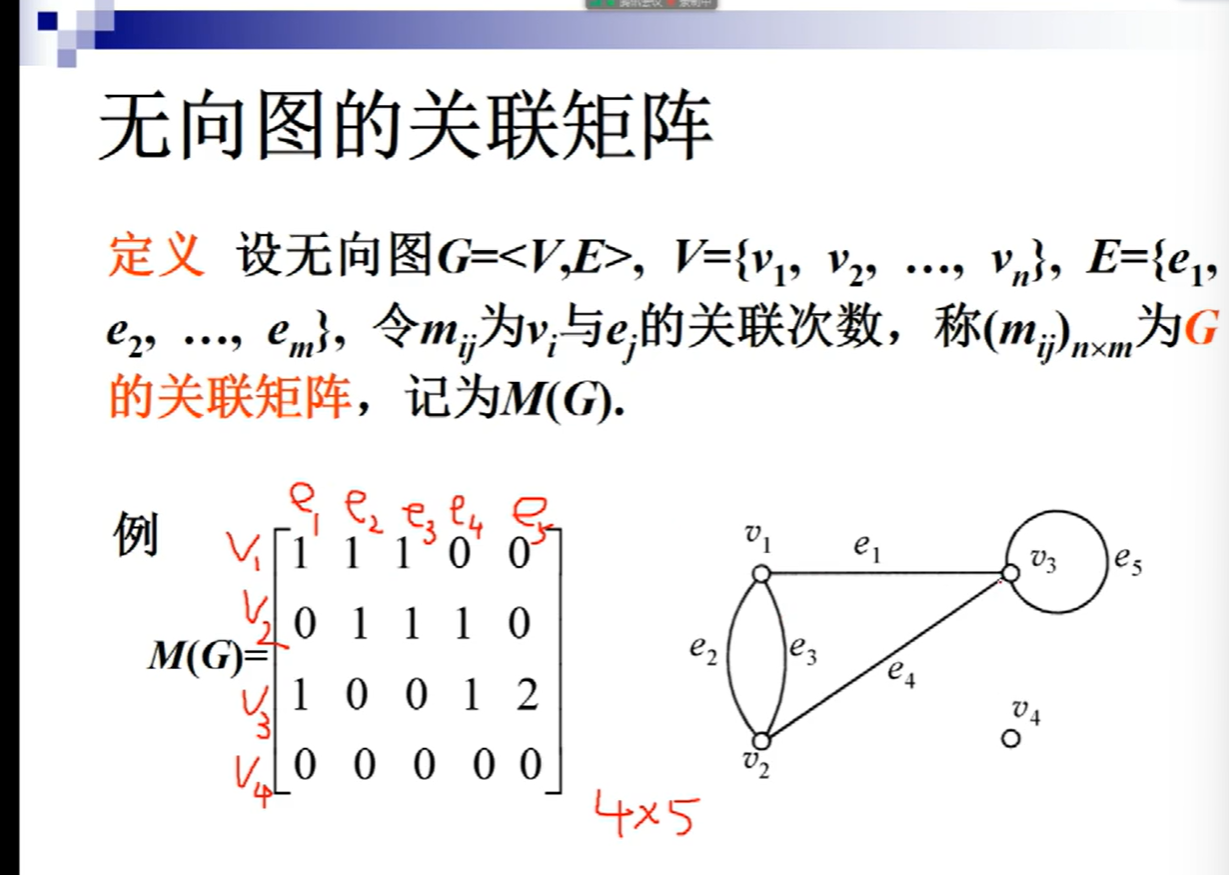
关联矩阵表示了图中点和边的关系,每一列中其实就对应了一个边
关联矩阵的特点:4*5意味着有4个点和5条边,如果是孤立点,则在矩阵中,这个点所在的行全是0
有向图的关联矩阵
有向要区分起点和终点,起点是1,终点是-1


每一列的和肯定是0,每一行的绝对值的和是这个点的度
有向图的邻接矩阵
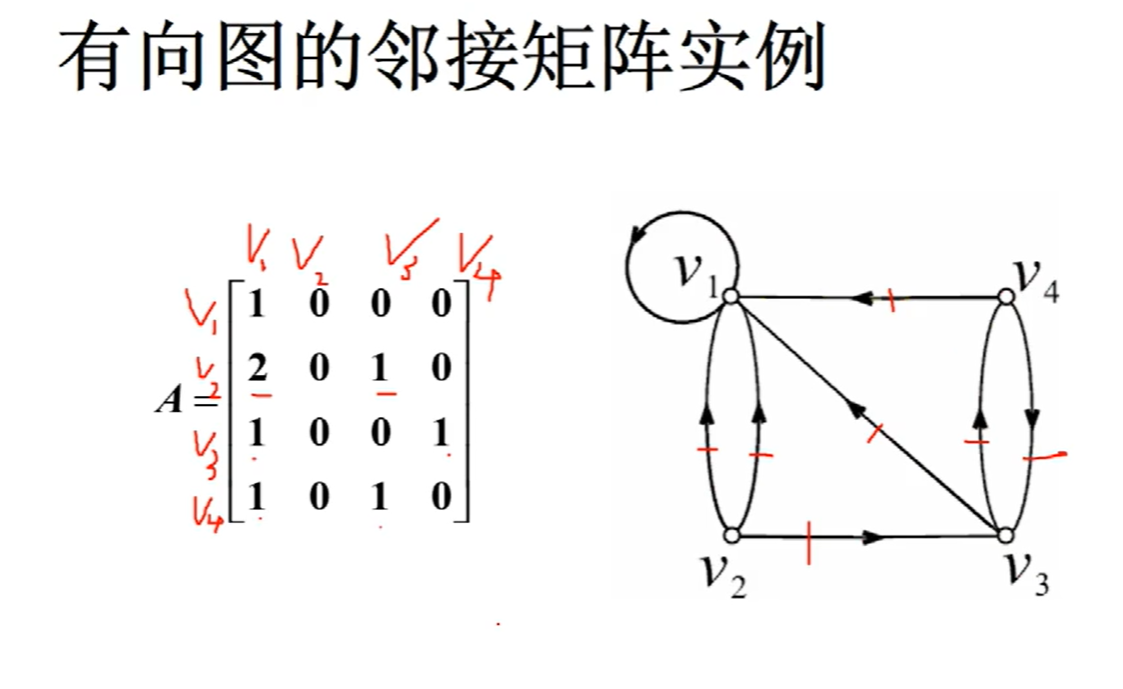
邻接矩阵一定是个方阵,方阵就可以用来计算
特点:每一行的和是这个点的出度,每一列的和是这个点的入度,将出度和入度相加,就是这个点的度
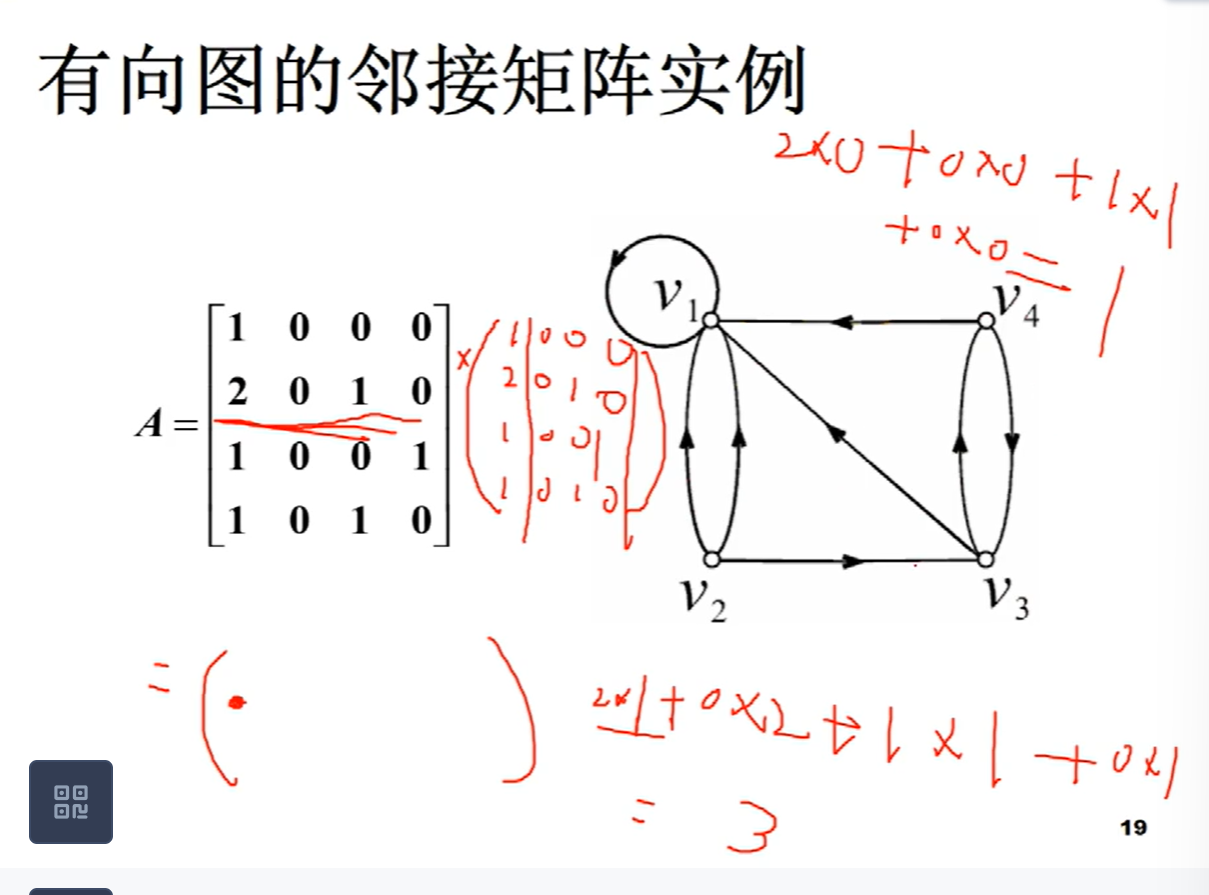
从v2到v4长度为2的通路只有1条
从v2到v1长度为2的通路有3条
回路的条数看主对角线
通路和回路条数的计算
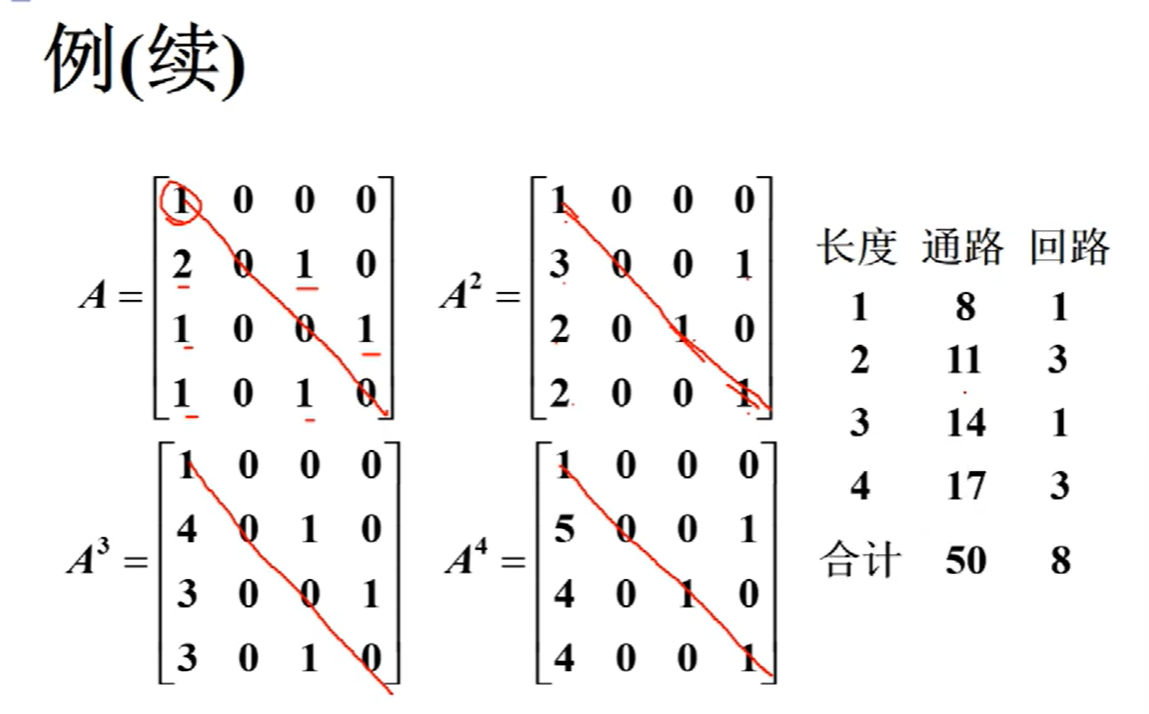
利用矩阵进行计算就行了
有向图的可达矩阵
可达矩阵的主对角线全是1
可达矩阵的计算:
逻辑的加减运算即可,最后主对角线都是1,说明是可达矩阵
注:矩阵是一种计数的方式
判断二部图
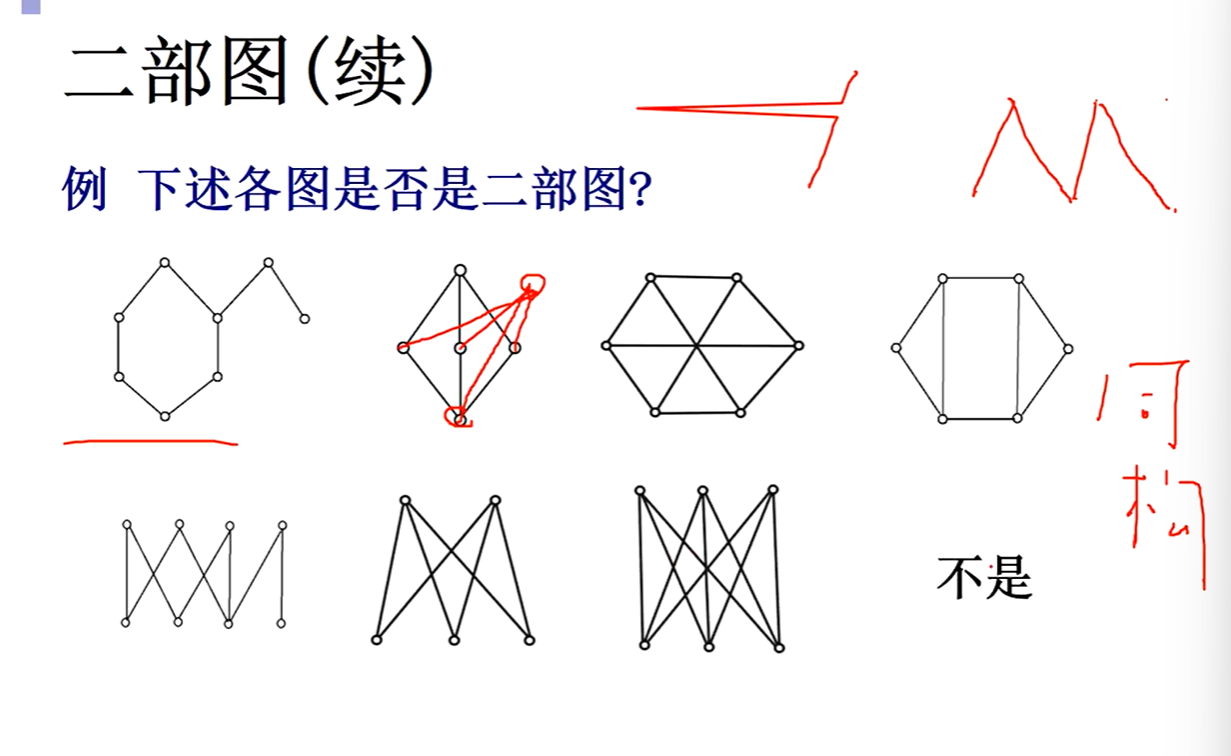
Kmn一共有m*n条边
二部图中没有长度为奇数的回路

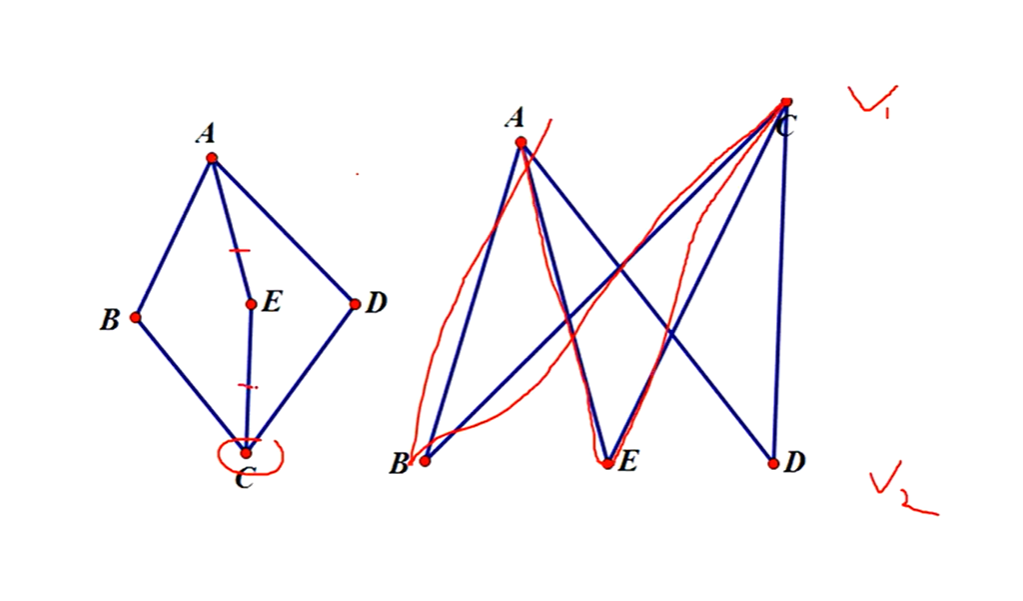
回路道路是AECB一共是四条边,如果是二部图,一定是偶数条边0.
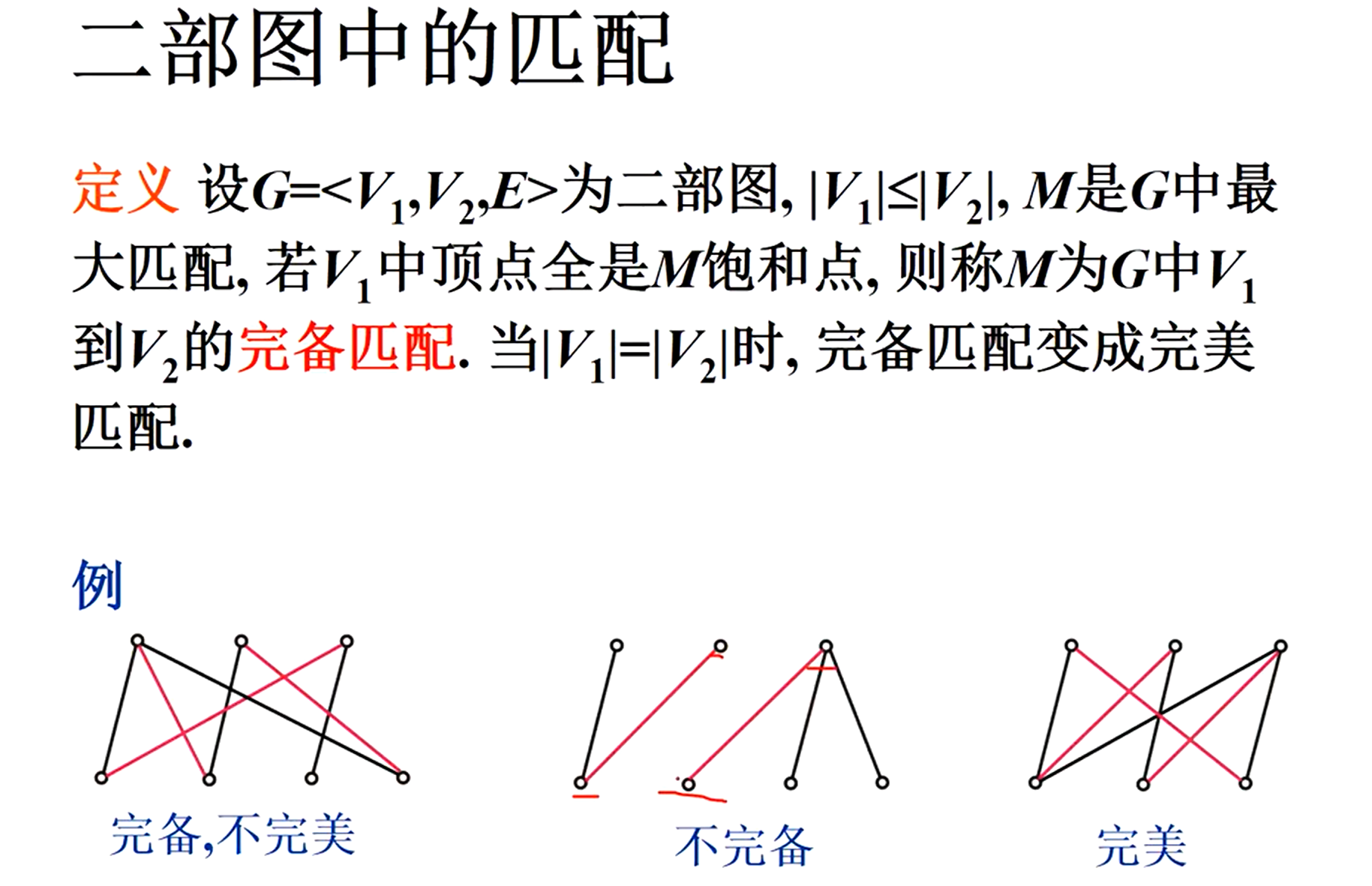
V1的个数和V2的个数是相同的,就可以构成完美匹配
欧拉图

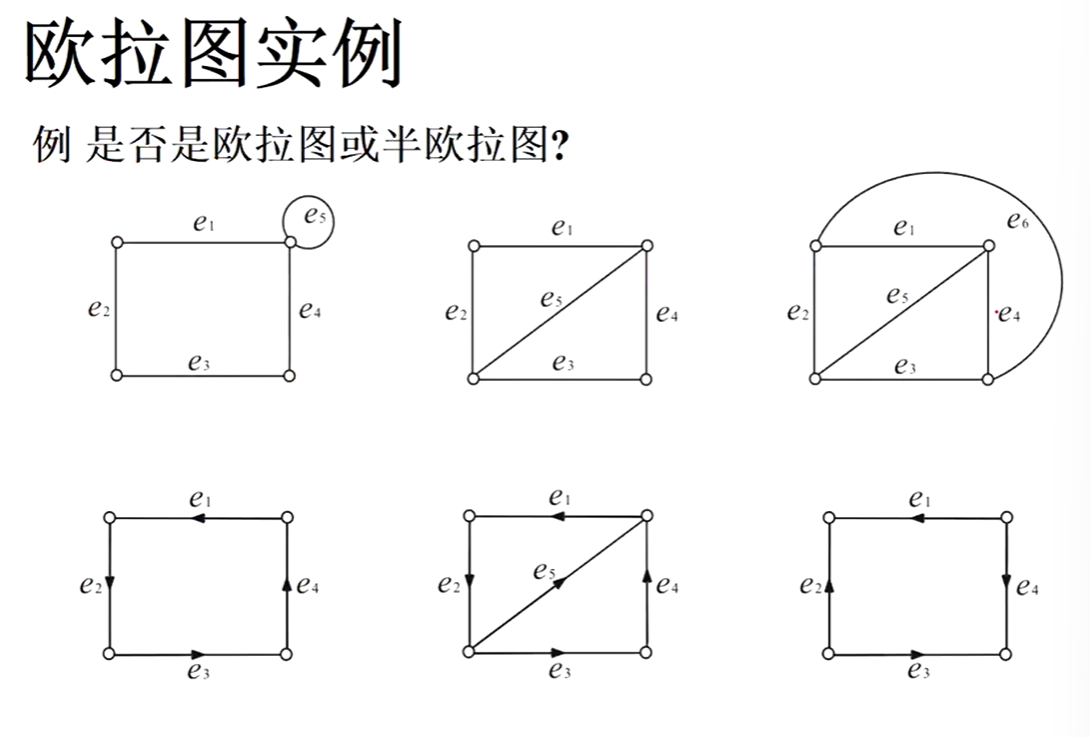
欧拉图的判别法
定理 无向图G为欧拉图当且仅当G连通且无奇度顶点。G是半欧拉图当且仅当G连通且恰有两个奇度顶点
定理 有向图D是欧拉图当且仅当D连通且每个顶点的入度都等于出度。D是半欧拉图当且仅当D连通且恰有两个奇度顶点,其中一个入度比出度大1,另一个出度比入度大1,其余顶点的入度等于出度
通俗说法:所有顶点的度都是偶数就是欧拉图;半欧拉图是个通路,它回不去
如何将半欧拉图变成欧拉图,将两个奇数度的点之间加上一条边,两个点的度就变成了偶数,于是就变成了欧拉图
哈密尔顿图
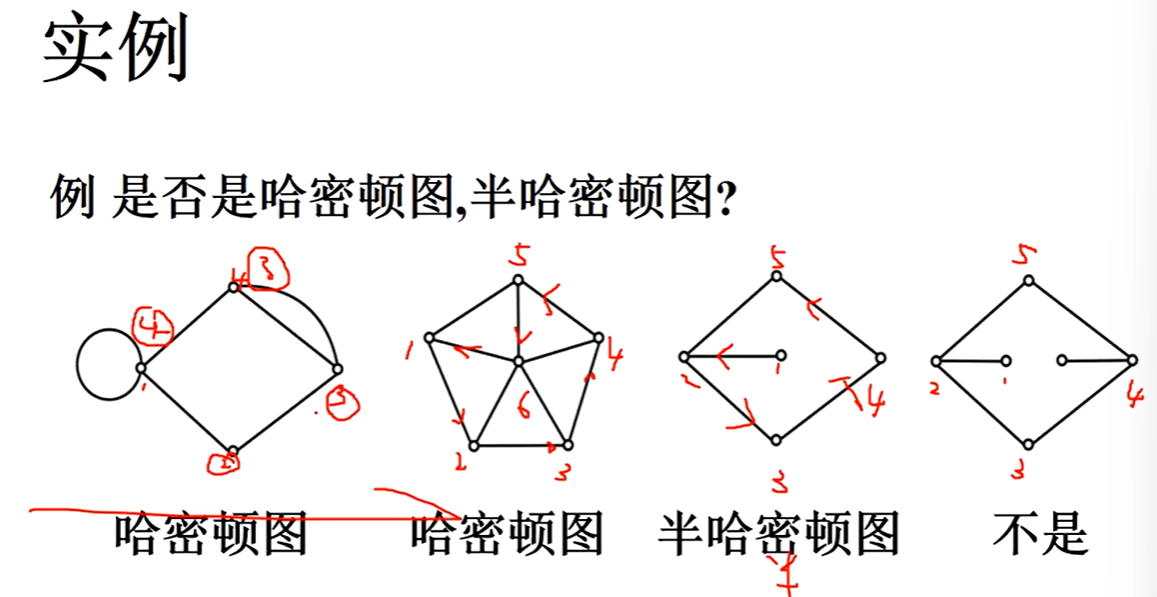
判断哈密尔顿图,没有严谨的判断方法

欧拉公式

VEF 点线面
树
树是一种特殊的图
无向树:无回路的连通无向图
平凡树:平凡图
森林:每个连通分支都是树的非连通的无向图
树叶:树中度数为1的顶点
分支点:树中度数≥2的顶点
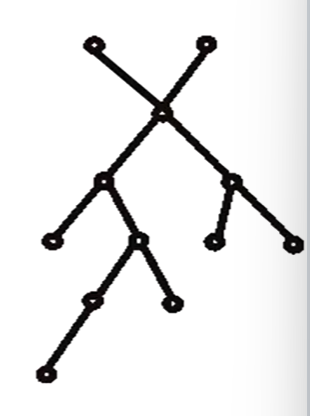
上图为一棵是12阶树
无向树的性质
